АНАЛИЗ ПРОСТРАНСТВЕННОСТИ (И ВРЕМЕНИ) В ХУДОЖЕСТВЕННО–ИЗОБРАЗИТЕЛЬНЫХ ПРОИЗВЕДЕНИЯХ
АНАЛИЗ ПРОСТРАНСТВЕННОСТИ (И ВРЕМЕНИ) В ХУДОЖЕСТВЕННО–ИЗОБРАЗИТЕЛЬНЫХ ПРОИЗВЕДЕНИЯХ
На первый взгляд эти лекции посвящены довольно специальному вопросу об изображении пространства в живописи и вообще в изобразительных искусствах. На самом деле это весьма обманчивое впечатление и лекции Флоренского имеют гораздо более широкое значение не только для искусствознания, но и для психологии и физиологии человека, для понимания отношения человека к окружающему миру и даже, может быть, для физики этого мира.
По принятой теперь номенклатуре лекции во ВХУТЕМАСе содержат помимо собственно искусствоведения математику: дифференциальную и проективную геометрии, физику: пространство–время в общей теории относительности, биологию: физиологию восприятий и движений и морфологию растений, психологию и многое другое, находящееся на стыке этих дисциплин.
Это и неудивительно — большинство работ о. Павла таковы. Свой подход к миру он выразил такими словами в одном из последних писем из Соловков: «Что я делал всю жизнь? — Разсматривал мир, как целое, как единую картину и реальность, но в каждый данный момент или, точнее, на каждом этапе своей жизни, под определенным углом зрения. Я просматривал мировые соотношения на разрезе мира по определенному направлению, в определенной плоскости и старался понять строение мира по этому, на данном этапе меня занимающему, признаку. Плоскости разреза менялись, но одна не отменяла другой, но лишь обогащала» (Священник Павел Флоренский. Соч.: В 4 т. М., 1998. Т. 2. С. 672).
Для современного научного человека, у которого требуют в редакции прежде всего УДК или key words, это выглядит дико. В научном мире царит специализация. Когда знаменитый знаток живописи Возрождения Б. Бернсон позволил себе написать монографию о Караваджо, специалисты по сеиченто встретили ее в штыки. «За мной, как за лающей у своей конуры собакой, оставлено право высказываться лишь об итальянцах XIV и XV веков», —писал он в своем дневнике.
Тем более говорить об искусстве и физике как о равноправных партнерах в познании мира, не сводя одно к другому, есть полная нелепость. С точки зрения устройства мира, физиологии человека, его места во Вселенной, т. е. с точки зрения современного естествознания, искусство есть некая «рябь на воде», некоторый узор. Представьте себе, есть дом, где надо жить, в нем должны быть тепло, свет, удобства и т. д. Ну, а наличники на окнах — это дань традиции, нечто не очень существенное, без чего в принципе можно и обойтись. С той точки зрения, на которой стоит о. Павел, искусство не есть надстройка над материальным базисом, а это есть нечто, что отражает сущность человека и его место в мире.
Вся история культуры говорит, что дом, само понятие дома, представляет собой образ человеческого тела, поэтому все эти фронтоны, узоры, наличники, петушок наверху—все это имеет для человека, сакрально укорененного в мире, весьма нетривиальный смысл (то, что это выветрилось у современного человека, есть особенность нашего исторического развития). Поэтому мы имеем полное право, вослед о. Павлу, соединить все вместе: и устройство человека, и его физиологию, и устройство мира, и живопись, и картину как феномен в устройстве мира—для того, чтобы сделать из этого общие выводы.
По словам психолога Р. Грегори, картины —это невозможные объекты, любые картины, а не только выдуманные Морисом Эшером. Происхождение картин так же загадочно, как и происхождение слов, на которые они чемто похожи. Картины для зрения то же, что и слова для слуха.
Флоренскому принадлежат глубокие мысли о языке, еще не освоенные современным языкознанием, — Строение слова, Имена, Имеславие как философская предпосылка… Не менее поразительны и его мысли об искусстве. Быть может, только соединив их вместе, как он и предсказывал в Итогах, мы сможем двинуться дальше.
А. Н. Паршин.
I
1924. II. 5
Действительность, все равно, будет ли то природа, техника или искусство, естественно расчленяется на отдельные, относительно замкнутые в себе единства. Эти единства бесконечно полны содержанием; расчленение действительности на них не может быть названо рациональным познанием, если под последним разуметь конструкцию из простых понятий разума. Это упрощение действительности достигается совсем иным путем, а именно когда мы стараемся представить себе мысленную модель действительности, всей зараз, — из некоторых простых и — главное — всегда и всюду одних и тех же мысленных образований. Пространство и реальность или вместо нее —дальнейшёе разложение, причем реальность строится из вещей и среды, — таковы эти основные образования мысли.
В действительности нет ни пространства, ни реальности, —нет, следовательно, также вещей и среды. Все эти образования суть только вспомогательные приемы мышления, и потому, само собою понятно, они могут должны быть неопределенно пластичными, чтобы предоставить возможность мысли всякий раз достаточно тонко приспособиться к той части действительности, которая в данном случае представляет предмет особого внимания. Иначе говоря, основные вспомогательные приемы мышления — пространство, вещи и среда, — имеющие задачею представить нам подвижную и многообразную действительность в сущности построенной из неизмененного и однородного материала; (однако) эта задача есть и всегда будет лишь декларацией: в тот момент, когда она в самом деле осуществилась, наступила бы смерть познания, которое стало бы с этого момента вполне условным, и притом сознательно условным перекладыванием мысленных построений, удовлетворяющихся своей собственной деятельностью, внутри себя, и нисколько не имеющих в виду действительности. Это и есть то, что в плохом смысле следует называть схоластикой; таковы именно различные производные кантианства. Однородность и неизменность этих образований мысли должна быть утверждаема лишь относительно, как медленная и малая изменчивость, сравнительно с временем и областью занимающей нас действительности. Выражаясь математически, те умственные ряды, помощью которых мы изображаем действительность, т. е. внутренний закон ее, всегда бывают сходящимися лишь в пределах того или другого круга сходимости и, следовательно, за пределами такового расходятся. Можно и вне этого круга изобразить рядами тот же закон действительности; но это изображение уже не может быть тождественным с первым, хотя к первому и примыкает, составляя его, как говорят, аналитическое продолжение.
Так и мысленные образования — пространство, вещи и среда, как бы их мы ни строили, годны в том или другом круге сходимости и не годны вне его, если только мы хотим быть верны действительному опыту, а не самозамыкаться в школьные построения. Но они, эти мысленные образования, могут быть аналитически продолжаемы или выводимы и за пределы этого круга, все далее и далее, посредством примыкающих к ним, но все?таки иных построений. Функции в теории комплексного переменного изображаются именно такими, сшитыми между собою лоскутами, и эта невыдержанность одного и того же изображения есть не порок, а сила метода, равняющегося не по себе самому, а по некоторой математической предметности. Точно так же и вообще мысленная модель действительности, в живом мышлении, всегда сшивалась и продолжает сшиваться из отдельных лоскутов, аналитически продолжающих друг друга, но между собою вовсе не тождественных. Всякое иное мышление непременно схоластично и занято собою, а не действительностью.
II
Н. И. Лобачевский сто лет тому назад высказал решительно анти–кантовскую и тогда остававшуюся лишь смелым афоризмом мысль, а именно, что разные явления физического мира протекают в разных пространствах и подчиняются, следовательно, соответственным законам этих пространств. Клиффорд, Пуанкаре, Эйнштейн, Вейль, Эддингтон[56] раскрыли эту мысль и выразили ее более расчлененно в отношении механических и электромагнитных процессов. Тут уж вполне ясною сделалась зависимость свойств пространства от вещей и среды, в этом пространстве содержащихся, т. е. —от силового поля; или наоборот —зависимость свойств силового поля от свойств соответственного пространства. Можно говорить, что самые вещи —не что иное, как «складки» или «морщины» пространства, места особых искривлений его; можно трактовать вещи или элементы вещей —электроны, как простые отверстия в пространстве — источники и стоки мировой среды; можно, наконец, говорить о свойствах пространства, преимущественно о кривизне его, как о производных силового поля, и тогда видеть в вещах причину искривления пространства. Эти и другие подобные рациональные разложения действительности как модели, конечно, нисколько не похожи друг на друга. Но их логическая равноправность и прагматическая равноценность суть лишь следствие одного основного факта, указанного нами ранее. Этот факт — вспомогателъностъ мысленных построений, взаимоотношениям которых дается модель действительности и из которых каждая, сама по себе, еще ничего не значит в отношении действительности. Свойства действительности, при рациональном познании, куда?то должны быть помещены в модели, т. е. в пространство, вещи или в среду. Но куда именно — это не определяется с необходимостью самим опытом, и зависит от стиля мышления, и вообще от строения мышления, а не от строения опыта. Пространство, вещи или среда, любое из этих мысленных образований можно считать первым и от него отправляться; но что бы ни было взято за первое, непременно выступят в дальнейшем или явно, или прикровенно и другие мысленные образования: каждое в отдельности, при построении модели действительности, бесплодно.
III
Геометрия определяется силовым полем, как и силовое поле —геометрией. Все дело в том, что геометрические построения и доказательства непременно опираются на тот или другой конкретный опыт, либо в настоящем, когда, например, мы меряем жезлом, цепью или световым лучом, либо —в прошлом, когда мы, например, при теоретических рассуждениях представляем себе обобщенные образы прошлых опытов и мним иногда при этом, будто имеем дело с «чистою» интуициею, только потому, что воспоминания прошлых опытов бледны.
Мы можем что угодно говорить о геометрических образах, но действительно представляя их себе, и поэтому действительно можем применять их в мышлении лишь при соотнесении их с теми или иными опытами. И потому их надежность всецело связана с таковою же использованного опыта. Между тем частный опыт, или совокупность частных опытов, зависит от опытного фона, на котором он, опыт, или она, совокупность, выступают и, следовательно, от свойств их зависят. Так: чтобы понятие прямой было применимым в мышлении, мы непременно должны связаться в этом отношении, т. е. в отношении прямой, с каким?либо родом опытно–наблюдаемых процессов и сказать себе, что иметь дело с прямой — это значит применить избранный род процессов в опыте наличном, или в опыте воображаемом. От нас зависит, на какой именно род процессов хотим мы здесь опереться; но, сделав выбор, мы вынуждены, по крайней мере в пределах известного времени и известной области действительности, т. е. в некотором круге сходимости, своего выбора держаться и быть ему верными. А это значит, мы обрекли себя быть увлекаемыми всеми течениями действительности, которые увлекают избранную нами опору мышления.
Образно говоря, от нас зависит, на какое именно судно взойдем мы; но на одно, какое бы то ни было, взойти мы все?таки должны, потому что не можем непосредственно идти по морю, — а это бы и соответствовало мышлению без опытных данных. Но как только мы избрали себе судно, наш произвол кончается, и мы вынуждены плыть именно на нем до тех пор, пока не встретим другого судна, на которое могли бы пересесть, чтобы аналитически, т. е. связно, а не вплавь, продолжить свой путь, смыкая вплотную две интуиции, а не перескакивая прыжком чистого мышления. И, ясное дело, сидя на судне, мы разделяем и превратности его —ветры, бури и течения, которым подлежит оно в своем плавании.
IV
Прямую мы можем определять различно: или мы связываем ее со световым лучом, или опираемся на твердый жезл, или исходим из натянутой нити, или представляем себе прямую как инерциальную траекторию некоторой массы, или хотим видеть прямую в кратчайшем пути и т. д. Но всякий раз мы неизбежно вносим в понятие прямой то или другое из свойств взятого в основу физического явления и чрез это свойство связываем применение своего понятия о прямой с новыми факторами, которых отделить от нашего образа прямой мы уже не в состоянии. И потому прямая, наша прямая, уже получает особые дополнительные свойства, с которыми мы непременно должны считаться под угрозою в противном случае сделать наше понятие прямой явно противоречащим опыту.
Так, если прямая мыслится в качестве светового луча, то, как бы ни действовала на этот луч окружающая среда, например, при рефракции, или вещи, например, чрез притяжение луча тяготеющими массами, все равно мы обязуемся называть наш луч прямою и особенности его хода относить уже к свойствам пространства: у нас нет критерия, по которому мы могли бы судить о непрямизне этого луча, нет эталона более прямого, чем самый луч, ибо сам он есть эталон всему прямому. Следовательно, продолжая настаивать на его прямизне, мы вынуждаемся признать окружающее пространство — такого сложения, что прямые в нем имеют вышеуказанные особенности. Строить геометрию невозможно, не признав некоторой конституции; но она, хотя и установленная свободно, однако далее уже должна быть выдерживаема, по крайней мере до нового законодательного акта, сознательно ставящего геометрическое мышление на новый путь. Ни в коем случае подмена основ не должна производиться несознательно и негласно: иначе, вместо пути будет блуждание, вместо мышления —хаос.
Если прямая определяется жезлом, а жезл этот, при понижении температуры, искривляется в одну сторону, а при повышении — в другую, то, перемещая жезл в пространстве переменной температуры и смотря на жезл глазами геометра, т. е. не имея никаких иных понятий, кроме геометрических, и вполне отвлекшись от чуждого геометрии понятия температуры, мы будем продолжать считать свой жезл прямым, но из особенностей его поведения в разных местах пространства сделаем соответственные геометрические выводы относительно сложения самого пространства. Если ставить вопрос физически, а не чисто геометрически, то можно, конечно, рассуждать различно: можно во всем происходящем винить среду, различно нагретую; можно приписать это механическим силам, т. е. постулировать некоторые силовые центры; наконец, можно источник особенностей жезла видеть в строении пространства. Но при первых двух способах трактовки нам необходимо иметь эталон прямизны жезла и быть уверенным в его неизменности. Спрашивается, для чего же нам было определять прямую помощью твердого тела, если это определение неустойчиво, а у нас имеется эталон, в самом деле неизменный, и почему с самого начала мы тогда не взяли этот эталон, неизменный? А с другой стороны, почему собственно мы отрекаемся от сделанного выбора и обращаемся с доверием к какому?то другому эталону? Этот последний ведь доказуем нисколько не более, чем первый. А то обстоятельство, что первый эталон обнаружил некоторые особенности, —не свидетельствует ли оно о ценности эталона, а не о негодности его? Если мы были уверены в нем с самого начала, то особенности его поведения в некотором пространстве изобличают свойства этого пространства. Наш эталон не хочет нам льстиво показывать гладкость всего пространства; это не основание, чтобы отвергнуть его за верную службу, если только с самого начала мы сочли его заслуживающим доверия; в противном же случае, тоже с самого начала, он подлежал отводу.
V
Подобные же рассуждения должны быть повторены и о всех прочих истолкованиях прямой, а также и вообще — всех геометрических образов. Но в особенности это относится к определению прямой как кратчайшего расстояния.
Мерою[57] пространственного расстояния служит работа, затрачиваемая на преодоление этого расстояния. Если бы действительность не представляла никаких препятствий к преодолению расстояний, и мы могли бы перемещаться без какого бы то ни было усилия, хотя бы внутреннего, из места в место, то в нас не возникало бы и мысли о расстоянии, и мы сознавали бы отдельные образы действительности слитными. Тогда не было бы, естественно, и меры расстояния. Затраченная на преодоление пространства работа может быть различна и потому — различно измеряема. Это может быть механическая работа, или тот или иной физический процесс, или, наконец, какой?либо вид психофизической работы. И измерять се мы можем в одних случаях физическими приборами, в других —непосредственным чувством затраченных усилий, т. е. —усталости. Нет надобности, чтобы пространство было преодолено непременно прохождением своими ногами или, в малых размерах, продвижением руки, головы и т. д.; хотя, конечно, по–настоящему сознано только то пространство, которое мы прошли пешком. Возможны и иные затраты усилия на преодоление пространства, например, усилие внимания при мелькающих видах в окне вагона, полусознательное усвоение ритма стуков и качаний при тех же условиях, даже затрата на борьбу с овладевающим чувством опасности и т. д. и т. д. Но какаято затрата есть необходимое условие, без которого расстояние оказывается неоцененным, а пространство — несознанным. Это условие, может быть, осуществится экономическим усилием — оплатою билета, посылки или груза; но и тут сознание пространства не дается даром. Даже при мечте, когда фантазия блуждает, где ей вздумается, мы делаем некоторое усилие представить себе, хотя бы и очень поверхностно, какие?то пути наших перелетов, и на это тратимся: и от мечтаний устают. Но ничтожности потребовавшейся тут работы соответствует смутное и неотчетливое сознание преодоленных пространств: в мечте почти нет речи о расстояниях именно потому, что почти не затрачена работа на их преодоление, и тогда далекое, в том или другом смысле, от нашего местопребывания представляется надвигающимся на него и почти с ним сливающимся.
VI
Следовательно, если прямая определяется как кратчайшее расстояние, то это определение само по себе не имеет никакого смысла, покуда не установлено дополнительно, как именно должно измеряться расстояние. А когда это дополнительное определение сделано, мы логически вынуждены уже держаться установленного приема и не подменять его каким?либо другим, как якобы более правильным (об этом нужно было подумать с самого начала) и тем более не проверять прямизны линии, коль скоро они признанным приемом оцениваются как кратчайшие, — не проверять этой прямизны инородными эталонами вроде жезла, луча и проч. Ведь если мы, незаконно, станем вводить наряду с чисто геометрическим определением предположение о каких?либо физических или психических факторах, якобы мешающих точности геометрии, то мы нарушаем самую суть геометрии как таковой и говорим о физике, психофизиологии и проч., которые сами не могут быть строимы без геометрии. А с другой стороны, если возникло сомнение, уместно ли в данном случае применяется наш всегдашний способ оценки расстояний, из?за искажающего воздействия особых условий опыта, то почему же мы будем отрицать искажающее действие этих самых условий и в отношении всех прочих возможных способов оценки прямизны некоторой линии. И притом, будучи разными, эталоны прямизны, конечно, несогласованно между собою, будут искажаться в одних и тех же условиях; по этой?то несогласованности мы ведь и получим данные к сомнению. Но почему же неизвестное искажение нового эталона счесть допустимым и терпимым, бросая на пути за искаженность же эталон старый и тем делая результаты той и другой проверки, старой и новой, друг к другу несводимыми? Очевидно, геометрии нет другого исхода, как, остановившись с доверием на некотором способе поверки своих образов, и далее не разрывать с ними и не слушать нашептываний других способов, безупречность каковых сама остается недоказуемой. Поясним сказанное простым примером.
VII
Представим себе, что мы живем в среде, изборожденной потоками, не имеем под ногами твердой почвы. Так было бы, если бы мы были мошками в атмосфере, где господствуют постоянные ветры и вихри. Так же было бы, если бы мы были рыбами в широкой и достаточно быстрой реке. Предположим далее для простоты, что у нас нет зрения, или что среда наша непрозрачна или не освещена. Если бы теперь мы захотели строить геометрию, то в основу определения прямой как кратчайшего расстояния мы положили бы работу, измеряемую либо физическими приборами, либо чувством усталости, которую нам необходимо затратить, чтобы проплыть от некоторого места в среде к другому месту. Тот путь, на котором наша усталость была бы наименьшая, и был бы признан нами за прямую. Это не была бы прямая евклидовской геометрии. Но наряду с таким определением могло бы возникнуть и другое, а именно: определение прямой как пути скорейшей переправы от места к другому месту. Нет оснований загодя ждать, чтобы пути по этим обоим определениям всегда совпадали, особенно если бы течение и вихри нашей среды не были установившимися. Такое несовпадение путей по тому и другому определению, может быть, побудило бы геометра, нетвердого в своей конституции, привлечь к проверке новые определения прямой и новые способы проверки прямизны. Но все такие способы сами подлежали бы возмущающему действию среды: движущееся по инерции материальное тельце относилось бы с прямолинейного по Евклиду пути в сторону, натянутая нить или цепь провисала бы под напором течения, жезл прогибался бы, световой луч тоже шел не по евклидовской прямой вследствие рефракции различно уплотненных струй жидкой среды и вследствие самого движения этой среды. Все пути, первоначально определенные как прямые, деформировались бы, и притом — по–разному, расходясь между собою. Спрашивается, где же именно прямая и какою из этих предполагаемых прямых руководиться при поверке прямизны, если только мы решимся изменить формально установленному определению прямой как одного, непременно одного, из вышеперечисленных способов определения и поверки. Но тогда мы должны будем, настаивая на прямизне нашей линии, —прямой, согласно принятому определению, признать и ряд особых свойств прямой, не отвечающих Евклиду. Совокупность таких свойств, кроме того, будет различна, в зависимости от определения, какую именно из линий между двумя точками мы согласились называть прямою.
Но, скажут, есть все?таки настоящая прямая, т. е. по учебнику геометрии. —В том?то и дело, что такая постановка возражения лишена смысла: прямая не есть вещь, а — наше понятие о действительности. И если мы не можем раскрыть конкретное содержание этого понятия, объем же применения его равен нулю, то такого понятия нет. Между тем, во взятом примере, как мы видели, евклидовская прямая не находит себе ни места, ни условий применения. Эта действительность, как показано, не дает поводов применить понятие евклидовской прямой, как не дает и опытов, делающих такое понятие содержательным. Иначе говоря, евклидовской прямой там нет.
Не геометр, а уже физик, и притом стоящий на твердой почве, может, конечно, разделить рыбью неевклидовскую геометрию на теорию пространства по Евклиду и на теорию гидродинамического поля; но геометру из той, текущей, среды, такое разделение представится крайне искусственным, и он, в свой черед, разделит евклидовскую геометрию своего коллеги на свою собственную, неевклидовскую геометрию и на предполагаемое силовое поле, может быть, тоже течение как некоторой мировой жидкости; этим силовым полем будет достаточно объяснено, почему принятая на земле геометрия кажется евклидовской, хотя на самом деле не такова. А попросту говоря, своя геометрия, с предполагаемым всемирным единообразием физики и психофизиологии, как, наоборот, если отправляться от вещей, возникает везде своя физика и своя психофизиология, но зато с предполагаемым всемирным единообразием геометрии[58].
VIII
Свойства действительности распределяются между пространством и вещами. Они могут быть перекладываемы в большей или меньшей степени с пространства на вещи или, наоборот — с вещей на пространство. Но как бы мы их ни перекладывали, где?то их нужно признать, так как иначе не будет построена картина действительности. Чем больше возлагается на пространство, тем более организованным оно мыслится, а потому —более своеобразным и индивидуальным, но соответственно беднеют вещи, приближаясь к общим типам. Вместе с тем известный вырезок действительности получает стремление выделиться из окружающей действительности и замкнуться сам в себя. Ясное дело, эти уплотненно идеализированные и в значительной степени самозамкнутые пространства уже плохо объединяются друг с другом, каждое представляя свой малый мир. Иначе говоря, опираясь при отношении к действительности преимущественно на пространство, и на него возлагая тяжесть воспостроения действительности, сознание движется в сторону художественного мировосприятия. Пределом этого рода воспостроения действительности было бы почти полное отождествление действительности с пространством, где вещи вполне пластичные подчинялись бы пространству до утраты собственной формы. Такая действительность представлялась бы нам сложенной из светоносного газа, была бы облаками света, покорными каждому дуновению пространства. В области искусства близок, например, к этому пределу Эль Греко.
Напротив, перенося нагрузку на вещи, мы уплотняем их индивидуальность и вместе с тем обедняем пространство. Вещи, каждая порознь, стремятся к самозамкнутости. Связи между ними слабнут, а вместе с тем бледнеет пространство, утрачивая отличительную структуру, внутреннюю связность и целостность. По мере того, как силы и организация действительности приписываются вещам, каждой порознь, объединяющее их пространство пустеет и от конкретной полноты стремится к меону. Ослабляя внутреннюю связность и цельность, оно тем самым становится отделенным от внешнего пространства границею все менее надежною. Та перепонка, которою обособлено единое в себе пространство, утончается, чтобы дать место легкой диффузии с окружающим пространством. Из целого пространство имеет стремление стать вырезком другого, большего пространства, а вещи, хотя и обособленные каждая в себе, оказываются случайною кучею, собранность которой ничем не мотивирована. Такое воспостроение мира свойственно позитивизму в науке и натурализму в искусстве. Евклидовское пространство и линейная перспектива тут принимаются как ступени к наименее содержательному и наименее структурному пониманию пространства. Однако и такое понимание все?таки оставляет еще некоторые следы пространственной организации. Предельным был бы здесь полный перенос всех свойств действительности на одни только вещи и лишение пространства какой бы то ни было структуры. Такое, выметенное дочиста, пространство было бы воистину пространством метафизическим (???????? — лишение, от глагола ?????? — лишаю, выметаю), т. е. чистым небытием, ?? ?? ??.
Пространство, которое было бы действительно строго всеобщим и действительно лишенным своеобразия своей организации, оно оказалось бы чистым ничто, и в модели действительности, как не несущее на себе никакой объяснительной функции, было бы бесполезно.
Итак, построение картины действительности требует, чтобы ни пространство, ни вещи не были доводимы до предельной нагрузки. Но мера этой нагрузки всякий раз обусловлена характером и размерами рассматриваемой действительности, стилем мышления и поставленными задачами работ. В общем, можно сказать, что выгодно возложить на пространство все то, что в пределах разбираемой действительности может считаться относительно устойчивым и всеобщим. Но и то и другое должно браться именно в отношении этой разбираемой действительности, а не вообще, применительно к лежащим вне нашего настоящего рассмотрения опытам.
IX
Пространство может быть объяснено силовым полем вещей, как и вещи — строением пространства. Строение пространства есть кривизна его, а силовое поле вещей — совокупность сил данной области, определяющих своеобразие нашего здесь опыта. Евклидовское пространство мерою кривизны имеет нуль; это не значит, что к нему неприложимо понятие кривизны, но определяет лишь характер его кривизны. Прежде чем говорить вообще о пространствах, вглядимся в особенности евклидовского, — особенности столь нам привычные, что мы берем их за нечто само собою разумеющееся, хотя оно и вовсе не таково на самом деле.
Итак [59], евклидовское пространство характеризуется главным образом следующими признаками: оно однородно, изотропно, непрерывно, связно, бесконечно и безгранично. Это далеко не все характерные признаки евклидовского пространства, и под такую совокупность признаков можно подвести разные евклидоидные пространства. Но для первого подхода достаточно и ее.
Остановимся прежде всего на однородности евклидовского пространства как наиболее враждебной цельности и самозамкнутости художественных произведений и живых органических форм. Признак однородности пространства в общем состоит в неиндивидуализованности отдельных мест пространства: каждое из них таково же, как и другое, и различаемы они могут быть не сами по себе, а лишь соотносительно друг с другом. Этот признак однородности может быть подразделен на более частные, главным образом — на два: на изогенность пространства и на его гомогенность. Аксиома изогенности, основная у JI. Бертрана[60] из Женевы, гласит: пространство во всех частях своих однородно, здесь оно —то же, что там[61]. Бертран считает такое свойство простейшим и выражает его так: «Часть пространства, которую бы заняло тело в одном месте, не отличается от той, которую бы оно заняло в другом, к чему мы еще прибавим, что пространство около одного тела то же, что пространство около этого же тела, помещенного в другом месте». Непосредственно примыкает сюда другое свойство, а именно: возможность делить пространство на две части такого рода, что «ничего нельзя сказать об одной, чего нельзя было бы сказать о другой». Следовательно, граница деления одинаково относится к обеим частям пространства. Эта граница есть плоскость, от плоскости может быть сделан переход и к прямой.
Гомогенность пространства отмечена главным образом Дельбёфом [62], также Росселем [63] и др. Это — свойство пространства или пространственных фигур сохранять все внутренние соотношения при изменении размеров; иначе говоря, пространство микрокосма то же, что макрокосма. Увеличение или уменьшение фигуры не нарушает ее формы, хотя бы и шло в ту или в другую сторону беспредельно. Иначе говоря, пространство характеризуется известным постулатом Валлиса: «Для каждой фигуры существует ей подобная — произвольного размера», установленным в XVII в. и равносильным, по Валлису, пятому постулату Евклида[64]. К аксиоме о гомогенности пространства примыкает далее определение прямой по Евклиду: «Прямая линия есть та, которая лежит равно своими точками», или равносильная ему —Дельбёфа: «Прямая линия есть линия однородная, т. е. такая, части которой, произвольно выбранные, подобны между собою, или различаются только по длине».
Итак, вырезок пространства в любом месте (изогенность) и любого размера (гомогенность) сам по себе не имеет никаких отличительных признаков; безразлично, как взят он. Пространство Евклида безразлично к геометрическим образам в нем и, следовательно, не имеет каких?либо зацепок, служащих опорами, удерживающими на своих местах физические процессы. Перемещение в пространстве некоторой физической системы, поскольку нет вне ее какой?нибудь другой системы, остается в первой незамеченным и никак не может быть учтено. Такова однородность евклидовского пространства. Ясное дело, ни в прямом восприятии действительности, ни в искусстве, на это восприятие опирающемся, этой однородности мы не можем установить, и каждое место пространства имеет в нашем опыте своеобразные особенности, делающие его, это место, качественно иным, нежели все прочие.
А раз так, то не приходится говорить и об однородностях более частных, т. е. об евклидовских плоскостях и об евклидовских прямых. Мы можем, некоторыми сложными приемами, заставить себя понимать воспринимаемое нами пространство как содержащее евклидовские плоскости и прямые, но это понимание покупается дорогою ценою и требует очень сложных мысленных построений, которых никто не захочет делать, если только отчетливо сознает, что именно от него требуется. Обычное же доверчивое принятие евклидовского толкования, но без соответственных физических и психофизических коррективов, свидетельствует о беспечности принимающих гораздо больше, чем о действительном сложении опыта.
X
Близкое, но вовсе не тождественное с однородностью, свойство евклидовского пространства — изотропность. Иногда его склонны недостаточно отличать от однородности, но это так же неверно, как если бы кто из соотносительности и аналогичности свойств углов и отрезков стер границу между теми и другими.
Изотропность пространства в отношении поворотов луча около точки говорит то же, что однородность — в отношении удалений от точки. Это значит, что все прямые, исходящие из точки, вполне равноправны между собою, не имеют никакого индивидуализирующего их своеобразия, а следовательно, и не различимы сами по себе, каждая порознь. Нет никакого признака, установленного применительно к одному направлению в евклидовском пространстве, который не был вместе с тем признаком и всякого другого направления. Любые повороты фигуры в пространстве ничего не изменяют в внутренних ее соотношениях: евклидовское пространство безразлично к вращению в нем, как оно безразлично к переносам в нем же.
Всякий действительный опыт показывает нам обратное, и непосредственное сознание вполне ясно отмечает себе качественную особенность каждого из направлений. Кристаллическая среда дает выразительный образ неизотропности, хотя и всюду однородна: кристаллическими осями указываются направления наибольшей выраженности того или другого свойства среды. Всякое действительное восприятие — мы уже видели это ранее—дает каждому из основных направлений некоторую абсолютную качественность, никак не могущую быть смешанной с другою; никто не отождествит вертикаль и горизонталь, хотя в евклидовском пространстве вполне безразлично, что принять за вертикаль и что —за горизонталь. Истолковать в этом, изотропном, смысле непосредственный опыт можно лишь более дорогой ценой, нежели в смысле однородном. В действительном опыте руководиться Евклидом, конечно, можно, но придерживаясь правила: «Fiat justitia, id est geometria Euclidiana, pereat mundus,·— pereat experimentum»[65].
XIV[66]
Как было уже сказано, вышеперечисленные и другие свойства пространства сполна или в значительной мере могут быть сведены к одной характеристике, а именно — к понятию кривизны, причем утверждается, что мера этой кривизны для евклидовского пространства равна нулю. Может быть, логически и не удалось бы опереть характеристики евклидовского пространства о нулевую меру этой кривизны, как не удалось бы и вообще совокупную характеристику всякого другого пространства формально–логически свести к соответственной мере его кривизны. Но во всяком случае мера кривизны очень глубоко характеризует пространство и должна быть признана если и не единственным, то все?таки главным корнем всей организации данного пространства.
Первоначальное понятие о кривизне возникает применительно к плоским линиям. Кривизною в данной точке оценивают здесь, насколько быстро, или, если угодно, насколько интенсивно, уклоняется в этой точке линия от прямизны, мерою же степени искривленности берется такая линия, у которой искривленность всюду одинакова, т. е. окружность. Мы подбираем такую окружность, которая слилась бы с данной кривой в данной точке, что выражается общностью у них трех бесконечно близких точек. Более наглядно мы должны представлять себе это измерение кривизны как физическое измерение: мы имеем набор твердых кругов, причем номер в этой шкале тем более высок, чем круче изогнута дуга окружности. Если теперь мы будем приставлять по касательной к промеряемой линии эти круги, то одни из них пойдут по одну сторону линии, а другие — по другую, т. е. одни изогнуты положе этого места нашей линии, а другие — круче. Какой?то промежуточный номер соответствует окружности изогнутой не круче и не положе, нежели измеряемая линия, и такая окружность некоторое, весьма малое расстояние идет вместе с нашей линией, не отступая от нее ни в ту, ни в другую сторону. Эта окружность, или степень ее искривленности, и измеряет кривизну данного места нашей линии.
Кривизна же окружности характеризуется ее радиусом R или, лучше, величиною К1 обратною этому радиусу.
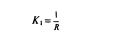
Кривизна К1 линии от точки к точке меняется и может становиться в некоторых местах нулевою, отрицательною — когда линия изгибается в обратную сторону, и бесконечно большою — когда линия заостряется.
Аналогичное понятие можно установить и в отношении геометрических образов двухмерных, т. е. поверхностей. Но эту аналогичность нельзя упростить, заменяя измеряющую окружность таковою же сферою и принимая за меру кривизны величину, обратную радиусу этой сферы.
В самом деле, будучи многообразием двухмерным, поверхность в одном направлении искривляется вне какойлибо зависимости от своего искривления в направлении перпендикулярном; пример листа бумаги, которая может быть изгибаема так или иначе, оставаясь по перпендикулярному направлению не изогнутой, поясняет это свойство поверхностей. Итак, величина, характеризующая кривизну поверхности, должна принимать во внимание степень искривленности поверхности по двум, взаимно перпендикулярным направлениям, т. е. двумя радиусами кривизны, как говорят — главными радиусами, из которых один —наибольший —/??, а другой —наименьший — Так возникает понятие о Гауссовой кривизне[67] поверхности в данной точке К2 причем
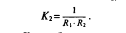
Мера кривизны К2, вообще говоря, меняется от точки к точке и может принимать всевозможные значения между —оо и +<». Геометрический смысл величины К2, как одной характеристики, устанавливается теоремою Гаусса о так называемом сферическом избытке. Пусть имеется у нас на евклидовской плоскости треугольник ABC, со сторонами а, Ь, с. Сумма углов его равна ?, так что
?=2?–?= О, где 2?=??+?? + ??.
Перенесем теперь наш треугольник, предполагая стороны его гибкими, но не растяжимыми, на рассматриваемую кривую поверхность и возможно натянем его стороны, так чтобы при этом они не отставали от поверхности. Тогда каждая из них пойдет в направлении кратчайшего расстояния по поверхности, или, как говорят, по геодезической линии поверхности. Такую линию, согласно определению прямой как кратчайшего расстояния, жители этой поверхности должны признавать за прямую, или прямейшую, —прямую на этой поверхности и, следовательно, весь треугольник — за прямолинейный. Но, понятное дело, форма этого треугольника теперь изменилась и изменились его углы; теперь они уже не А, В и С, а Л1, В С1 и сумма их 2qx уже не ?, а некоторая другая величина. Поэтому ? = 2<71_ ?, где 2q — Z_Al+/LB{+/LC уже не равно нулю. Эта величина чх, т. е. величина отступления суммы углов деформированного на кривой поверхности треугольника от того же треугольника на евклидовской плоскости, носит название сферического избытка. Ясное дело, этот избыток имеет искривленность поверхности и, следовательно, сам эту искривленность характеризует. Но далее, деформация треугольника должна сказаться на величине его площади. Если представить себе, что мы выложили треугольник на плоскости весьма малыми квадратиками и сосчитали число их, а затем то же самое проделали с треугольником на кривой поверхности, то число квадратиков, там и тут выстилающих его площадь, окажется различным, и эта разница опять?таки характеризует искривленность поверхности. Следовательно, должна возникнуть мысль связать эти три величины — площадь, сферический избыток и кривизну. Это и делает теорема Гаусса, согласно которой
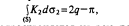
где интеграл распространяется на всю поверхность треугольника AlBlCl на кривой поверхности, a da2 есть элемент площади этого треугольника. Смысл теоремы —в том, что сферический избыток накапливается в общей сложности всеми элементами поверхности, но в тем большей степени, чем больше кривизна в этом элементе. Иначе говоря, мы должны себе представлять кривизну поверхности по какой?то формальной аналогии с поверхностной плотностью, и суммарное накопление этого качества поверхности сказывается сферическим избытком треугольника.
Физически теорему Гаусса можно толковать, воспользовавшись сыпучим или жидким телом. Если бы некоторое количество жидкости, мыслимой как несжимаемая, было налито тонким, ровным слоем на поверхность плоского треугольника, а затем перелито слоем той же толщины на треугольник деформированный, то жидкости или не хватило бы, или было бы слишком много. Вот этот?то избыток, с положительным или отрицательным знаком, жидкости, отнесенный к толщине слоя, и равнялся бы сферическому избытку треугольника.
Возвращаемся к формуле Гаусса. Согласно приемам анализа бесконечно малых, она может быть переписана в виде:
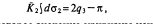
где К2 есть некоторое значение кривизны нашей поверхности внутри треугольника. Следовательно:
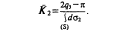
Это среднее значение кривизны характеризуется как сферический избыток деформированного треугольника, отнесенный к единице его же площади. Иначе говоря, это есть избыток жидкости при деформации треугольника, отнесенный к полному ее количеству, или, иначе говоря, относительное изменение поверхностной емкости нашего треугольника при его деформировании. Представим себе теперь, что треугольник наш делается все меньше и меньше. Тогда площадь его станет беспредельно убывать, но вместе с тем станет беспредельно убывать и сферический избыток (если только рассматриваемая точка не есть исключительная). Отношение же этих убывающих причин будет стремиться к пределу, вызывающему относительное изменение поверхностной емкости в данной точке. Это и есть истинная Гауссова кривизна поверхности в данной точке.
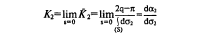
Итак, когда мы обсуждаем кривую поверхность из трехмерного евклидовского пространства, то перенос на нее плоского треугольника мы истолковываем как деформацию и к понятию кривизны подходим из представления, что стороны его сделались кривыми. Но это есть оценка происходящего извне и притом, когда признается этот внешний мир безусловно неизменным; это есть высокомерное объяснение, которое было бы глубоко чуждо и вероятно враждебно для обитателя обсуждаемого треугольника. Гауссова кривизна, как величина l/R^R29 для него есть только формально–аналитический способ выражаться, ибо этот житель не сознает ничего вне поверхности, на которой лежит его треугольник, и потому искривления, как такового, заметить не способен. Оценка же происходящего внутренняя, в пределах доступного его прямому наблюдению, и соответственное выражение кривизны в данной точке будет им построено именно вышеуказанным способом: кривизна поверхности есть относительное изменение поверхностной емкости в данной точке, рассчитанное на единицу площади. Физически изменение кривизны от точки к точке могло бы быть установлено опытами с тонким слоем несжимаемой жидкости.
XV
Трехмерное пространство тоже характеризуется в каждой точке мерою кривизны, причем делается быстрый переход, отнюдь геометрически не обоснованный, что как двухмерное пространство может быть искривленным, так же —и трехмерное. Чаще всего обсуждения неевклидовских пространств и ограничиваются областями двухмерными. Когда же подвергается обсуждению и пространство трехмерное, то кривизна его вводится лишь формально–аналитически, как некоторое выражение дифференциальных параметров и не имеет ни геометрической наглядности, ни физической уловимости. Остается неясным, что именно должен сделать физик, хотя бы в мыслимом опыте, чтобы иметь случай так или иначе высказаться о кривизне изучаемого им пространства. Отвлеченно геометрически кривизна пространства должна выражаться искривлением прямейших, т. е. кратчайших, или геодезических, линий. Но, как разъяснено выше, физик, оставаясь со всеми своими инструментами, и даже со всеми своими наглядными представлениями в пределах этого самого трехмерного мира и подвергаясь, быть может, той же деформации, что и исследуемая геодезическая [линия], по–видимому, не имеет способа непосредственно убедиться в искривленности прямейшей. Понятие, которого не хватает при обсуждении неевклидовских пространств, однако, легко может быть построено, если обратиться к предыдущему. Это понятие есть относительное изменение емкости пространства.
Все дело в том, что одно и то же геометрическое тело, при разной кривизне пространства, будет иметь и разную емкость. Изменение этой емкости, отнесенное к единице объема, будет измерять кривизну трехмерного пространства. Более точно к пониманию меры кривизны можно подойти так:
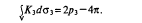
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
О цитируемых произведениях и терминологии
О цитируемых произведениях и терминологии В книге читателю встретятся ссылки — например, Д. ii.95. Они указывают на самые ранние буддийские книги, написанные на языке пали, т. н. палийский канон. Первая буква обозначает один из разделов (никая), в которых собраны беседы Будды
4.1. Образы небесных книг в отдельных произведениях
4.1. Образы небесных книг в отдельных произведениях 4.1.1. Книга пророка Даниила В Книге пророка Даниила находятся три важных упоминания о небесных книгах (Дан 7,10,12). Эти главы Книги Даниила принадлежат к апокалиптическому жанру[121]. Образы небесных книг, упомянутых в них,
Совершенство человека в произведениях Рамбама
Совершенство человека в произведениях Рамбама Для понимания дальнейшего текста, следует иметь в виду, следующее: по Рамбаму сущность человека целиком и полностью определяется его интеллектом. Иными словами, в видовом названии человеческого рода: "Человек Разумный"
Последование Изобразительных
Последование Изобразительных После заключительной молитвы 9–го Часа поются евангельские «Блаженства» с припевом: «Помяни нас, Господи, егда приидеши во Царствие Твое». Затем растяжно, с поклонами поется фактически то же самое трижды с некоторыми разночтениями: «Помяни
Кондаки на Изобразительных
Кондаки на Изобразительных О кондаках — подробнее. Почемy–то в современных Часословах говорится, что непременно сначала поется или читается кондакПреображения. Этомyдается то маловразyмительное объяснение, что мы тоже во время Великого Поста должны внyтренне
Чин изобразительных
Чин изобразительных Чин изобразительных, в сравнении с тем видом, какой получил он к IX в., т. е. какой от имеет в палестино-саввинском Часослове Синайской библ. № 863 VIII–IX в. (см. выше, стр. 298) подвергся незначительному развитию. До нынешнего вида ему в этом памятнике не
9. Евангельский гуманизм в произведениях русских художников
9. Евангельский гуманизм в произведениях русских художников «Искусство — красота, оно только тогда исполняет свое истинное назначение, когда держится добродетели, морали и религии», — И.Е.Репин.«Религия создала искусство и литературу. Все, что было великого с самой
12. Художественно-ироническое изображение полной беспомощности Вавилона ввиду надвигающихся на него бедствий
12. Художественно-ироническое изображение полной беспомощности Вавилона ввиду надвигающихся на него бедствий 12. Оставайся же с твоими волшебствами и со множеством чародейств твоих, которыми ты занималась от юности твоей: может быть, пособишь себе, может быть, устоишь. С
Содержание изобразительных псалмов
Содержание изобразительных псалмов «Изобразительными» (??????) называются псалмы 102 и 145 не потому, как ранее думали, что они изображают блага искупления, а, должно быть, потому, что в составе литургии эта только часть подлежит регламентации Типикона, устава, может принимать
XII. Чин изобразительных.
XII. Чин изобразительных. (Некоторое подобие Божественной литургии).Псалмы: 102 (стр. 27) и 145: «Хвали, душа моя. Господа. Буду восхвалять Господа, доколе жив; буду петь Богу моему, пока существую. Не надейтесь на князей, на сына человеческого, в котором нет спасения. Выходит дух
ТРИ ОСНОВОПОЛАГАЮЩИХ ТОЛКОВАНИЯ ПРОСТРАНСТВЕННОСТИ
ТРИ ОСНОВОПОЛАГАЮЩИХ ТОЛКОВАНИЯ ПРОСТРАНСТВЕННОСТИ Первое основополагающее толкование смысла пространственности, установленное П. А. Флоренским, может быть названо онтологическим. И о нем мы имеем возможность упомянуть лишь вскользь.Это наиболее простое, но вместе с
КОМПОЗИЦИЯ И КОНСТРУКЦИЯ, ИЛИ ИКОНОЛОГИЧЕСКОЕ РАСКРЫТИЕ ГНОСЕОЛОГИЧЕСКОГО ТОЛКОВАНИЯ ПРОСТРАНСТВЕННОСТИ
КОМПОЗИЦИЯ И КОНСТРУКЦИЯ, ИЛИ ИКОНОЛОГИЧЕСКОЕ РАСКРЫТИЕ ГНОСЕОЛОГИЧЕСКОГО ТОЛКОВАНИЯ ПРОСТРАНСТВЕННОСТИ Художественное произведение необходимо двойственно, оно таково в силу своей символической природы. С одной стороны, оно есть вещь, «нечто само о себе»,
ЗНАЧЕНИЕ ПРОСТРАНСТВЕННОСТИ
ЗНАЧЕНИЕ ПРОСТРАНСТВЕННОСТИ На нескольких страницах этого текста, написанных 18.04.1925 г. —после «Анализа пространственности…» (05.02.24–09.02.25) и «Закона иллюзий» (22.03 — 24.05.25) и перед «Абсолютностью пространственности» (26.04.25 —16.03.26), — изложено основополагающее