Приложение С Рок чисел
Приложение С
Рок чисел
Законы, правящие числами, озадачивают неподготовленный ум, а результаты, которые получаются при подсчетах, бывают поразительными. Поэтому нет нужды удивляться тому факту, что числа сопровождают всякие предрассудки.
Но даже для тех, кто знаком с исчислениями, существует множество загадочных и необъяснимых вещей, которые убедительно может объяснить только хороший математик. Простой человек видит, что числа подчиняются определенным законам, но не понимает, почему так происходит, и сам факт этой невозможности объяснить способствует тому, что вокруг чисел возникает атмосфера загадочности, внушающая благоговение.
Например, особенности числа 9, открытые, как я полагаю, В. Грином, который умер в 1794 году, являются необъяснимыми для всех, кроме математиков. Свойство, о котором я говорю, состоит в том, что когда 9 умножается на 2, 3, 4, 5, 6 и так далее, то простые числа, составляющие произведение, при сложении дадут девять. Итак:
2 ? 9 = 18, а 1 + 8 = 9
3 ? 9 = 27, а 2 + 7 = 9
4 ? 9 = 36, а 3 + 6 = 9
5 ? 9 = 45, а 4 + 5 = 9
6 ? 9 = 54, а 5 + 4 = 9
7 ? 9 = 63, а 6 + 3 = 9
8 ? 9 = 72, а 7 + 2 = 9
9 ? 9 = 81, а 8 + 1 = 9
10 ? 9 = 90, а 9 + 0 = 9.
Заметим, что 9 ? 11 дает 99, и сумма чисел в этом случае равна 18, а не 9, но зато при сложении 1 и 8 получается 9.
9 ? 12 = 108, и 1 + 0 + 8 = 9
9 ? 13 = 117, и 1 + 1 + 7 = 9
9 ? 14 = 126, и 1 + 2 + 6 = 9
И так далее до бесконечности.
Господин де Меван открыл другое свойство того же числа 9. Если поменять местами цифры, составляющие некое число, и вычесть полученное число из первоначального, то разность будет равна или же кратна 9 и сумма чисел, составляющих эту кратную 9 разность, будет также равна 9.
Например, возьмем число 21, поменяем цифры местами и получим 12, вычтем 12 из 21, разность будет равна 9. Возьмем 63, переставим цифры и отнимем 36 из 63, получим 27, кратное 9, а 2 + 7 = 9. Теперь возьмем 13, преобразовав его, получим 31, разность этих чисел составляет 18, то есть дважды девять.
Такое же свойство, наблюдаемое у двух чисел, измененных подобным образом, обнаруживается у тех же чисел, возведенных в степень.
Возьмем снова 21 и 12. 21 в квадрате дает 441, а квадрат 12 равен 144. Разность при вычитании 144 из 441 составляет 297, кратное 9. Кроме того, числа, составляющие результаты этих возведений в степень, при сложении дают 9. 21 в кубе равно 9261, а 12 в кубе будет 1728, их разность составляет 7533, кратное 9.
Число 37 также имеет некоторые замечательные свойства, когда его умножают на 3 или на число кратное 3 (до 27). Произведение в этом случае составляют три одинаковые цифры. Зная об этом свойстве числа 37, искать произведение становится проще, ибо достаточно просто умножить первую цифру умножаемого на первую цифру множителя[133]. Дальнейшее умножение уже бессмысленно, поскольку достаточно просто написать справа от полученной цифры такую же цифру еще дважды – ибо одна и та же цифра будет занимать место единицы, десятка и сотни.
Приведем для примера следующую таблицу:
37, умноженное на 3, дает 111, а 3, умноженное на 1, равно 3,
37, умноженное на 6, дает 222, а 3, умноженное на 2, равно 6,
37, умноженное на 9, дает 333, а 3, умноженное на 3, равно 9,
37, умноженное на 12, дает 444, а 3, умноженное на 4, равно 12,
37, умноженное на 15, дает 555, а 3, умноженное на 5, равно 15,
37, умноженное на 18, дает 666, а 3, умноженное на 6, равно 18,
37, умноженное на 21, дает 777, а 3, умноженное на 7, равно 21,
37, умноженное на 24, дает 888, а 3, умноженное на 8, равно 24,
37, умноженное на 27, дает 999, а 3, умноженное на 9, равно 27.
Исключительные свойства разных чисел, которые при сложении дают одинаковую сумму, послужили причиной использования магических квадратов в качестве талисманов. Хотя все можно объяснить с точки зрения математики, многие авторы писали о них как о «загадочных».
Я приведу три примера магических квадратов:
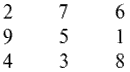
Эти девять цифр, расположенных по горизонтали, дадут в сумме в каждом ряду 15. Если сложить числа в каждой колонке, тоже получится 15. И при сложении трех цифр, составляющих каждую диагональ, сумма будет равна 15.

Лишь связи определенных чисел с религиозными догмами, даже если не принимать во внимание их необыкновенных свойств, оказалось достаточно, чтобы породить различные суеверия. Поскольку на Тайной вечере за столом присутствовало тринадцать человек и один из них предал своего Учителя, а затем повесился, то у христиан считается несчастливым, когда за столом сидит тринадцать обедающих, ибо это означает, что один из них умрет прежде, чем закончится год. Вовенарг сказал: «После того как я увидел, как тринадцать гениальных людей не осмеливались сесть за стол, поскольку их было тринадцать, никакие заблуждения прошлого и настоящего меня не удивляют».
Девять, священное число в буддизме, окружено благоговением среди монголов и китайцев, последние кланяются девять раз, представая перед своим императором.
Три считается священным у индуистов и христиан из-за триединства Бога.
Пифагор учил, что каждое число обладает своим характером, достоинствами и свойствами.
Он говорил: «Единица, или монада, – это первопричина и конец всего, это звено, которое связывает воедино цепь причин, это символ тождества, равенства, существования, сохранения и всеобщей гармонии. Не будучи делимой, монада воплощает Божественность, она предвещает также порядок, мир и покой, которые основаны на единстве чувств. Соответственно, ЕДИНИЦА – это хорошее начало».
«Число ДВА, или диада, – начало противоположностей, является символом многообразия, или неравенства, разделения и разъединения. Следовательно, два – это злое начало, число, предвещающее несчастье, характеризующее хаос, беспорядок и изменение».
«ТРИ, или триада, – это первое нечетное число, содержащее величайшие тайны, поскольку все состоит из трех веществ; оно представляет Бога, душу мира, дух человека». Это число, которое играло большую роль в преданиях Азии и платонической философии, выражает свойства Бога.
«ЧЕТЫРЕ, или тетрада, как первая математическая степень, является одним из главных элементов; оно представляется образующей силой, из которой происходят все комбинации, это самое совершенное из всех чисел, которое является основой всех вещей. Оно священно по своей природе, ибо составляет сущность Бога; оно возвращает Его единство, Его силу, Его доброту и Его мудрость – четыре совершенства, которые характеризуют Бога. Соответственно, пифагорейцы клянутся четверичным числом, которое дает человеческой душе ее вечную природу».
«Число ПЯТЬ, или пентада, имеет особую силу в священном искуплении; оно является каждой вещью, оно останавливает силу ядов и вызывает страх у злых духов».
«Число ШЕСТЬ, или гексада, является счастливым, оно приобрело свои достоинства от первых скульпторов, которые разделили лицо на шесть частей. Однако, согласно халдеям, причина в том, что Бог создал мир за шесть дней».
«СЕМЬ, или гептада, является очень действенным числом и для добра, и для зла. Оно принадлежит, главным образом, священным вещам».
«Число ВОСЕМЬ, или октада, является первым кубом, то есть квадратно во всех отношениях, как игральная кость, оно исходит из своего основания, двойки, четного числа. Таков и человек, четырежды квадратный или совершенный».
«Число ДЕВЯТЬ, или эннеада, будучи кратным числу три, должно рассматриваться как священное».
«И наконец, ДЕСЯТЬ, или декада, является мерой всего, поскольку содержит все числовые отношения и гармонии. Как воссоединение первых четырех чисел, оно играет значительную роль, поскольку все науки и все названия происходят из него и в него же уходят».
Едва ли мне стоит сделать больше, нежели просто упомянуть об особенных значениях чисел, которыми наделяет их христианство. Единица – это числовое выражение Единства Бога, Два – двойственной природы Христа, Три – Святой Троицы, Четыре – евангелистов, Пять – числа святых ран Господа нашего Иисуса Христа, Шесть – это число греха, Семь – даров Святого Духа, Восемь – Заповедей блаженства, Десять – число заповедей, Одиннадцать – количество апостолов после ухода Иуды, Двенадцать – общее число учеников Христа.
А теперь я расскажу о некоторых числах, которые рассматривались сквозь призму предрассудков, а также о вызывающих особый интерес определенных событиях, которые с ними связаны.
Считается, что число 14 оказывало необычное влияние на жизнь Генриха IV и других французских правителей. Обратимся к истории Генриха.
14 мая 1029 года первый король по имени Генрих был помазан на царство, и 14 мая 1610 года последний монарх с таким же именем был убит.
Четырнадцать букв[134] входит в состав имени Генриха Бурбона, который был четырнадцатым монархом, носившим титул короля Франции и Наварры.
Генрих IV родился 14 декабря 1553 года, то есть через 14 веков, 14 десятилетий и 14 лет после рождения Христа. Если сложить вместе цифры, составляющие его год рождения, то сумма будет равна 14.
14 мая 1554 года Генрих II повелел расширить улицу Медников, но приказ так и не был приведен в исполнение. Из-за этого убийца Генриха IV смог осуществить свой замысел на этом месте, четыре раза по четырнадцать лет спустя.
14 мая 1553 года родилась Маргарита де Валуа, первая жена Генриха IV.
14 мая 1588 года в Париже началось восстание против Генриха III, организованное герцогом де Гизом.
14 марта 1590 года Генрих IV выиграл битву при Иври.
14 мая 1590 года атака Генриха IV под Парижем была отражена.
14 ноября 1590 года Шестнадцать поклялись скорее умереть, чем служить Генриху.
14 ноября 1592 года в парламенте была оглашена папская булла, дающая легату власть назначать короля, за исключением Генриха.
14 декабря 1599 года герцог Савойский примирился с Генрихом IV.
14 сентября 1606 года произошло крещение дофина – будущего короля Людовика XIII.
14 мая 1610 года короля задержали на улице Медников: его карета не смогла разминуться с другой повозкой из-за узости этой улочки. Равальяк воспользовался преимуществом и нанес монарху удар кинжалом.
Генрих IV прожил четыре раза по 14 лет, 14 недель и 4 раза по 14 дней, то есть 56 лет и 5 месяцев.
14 мая 1643 года умер Людовик XIII, сын Генриха IV. Это произошло в тот же день и месяц, как и у его отца; если сложить цифры, составляющие год (1643), то сумма будет равна 14, так же как при складывании цифр года рождения его отца получится 14.
Людовик XIV взошел на трон в 1643 году:
1 + 6 + 4 + 3 = 14.
Он умер в 1715 году: 1 + 7 + 1 + 5 = 14.
Он прожил 77 лет, а 7 + 7 = 14.
Людовик XV взошел на трон в том же году, а умер в 1774 году, что также несет отпечаток числа 14: крайние цифры, поставленные вместе, образуют число 14, и сумма средних (7 + 7) равна 14.
Людовик XVI правил уже 14 лет, когда он созвал Генеральные штаты; это вызвало революцию.
Число лет, прошедших между убийством Генриха IV и свержением Людовика XVI, кратно 14.
Людовик XVII умер в 1794 году, крайние цифры даты вместе составляют число 14, а первые две дают его «порядковый номер».
Восстановление монархии Бурбонов произошло в 1814 году, крайние цифры вновь формируют число 14, и результат сложения всех цифр дает 14.
Ниже приводятся другие любопытные подсчеты, касающиеся отдельных французских королей.
Если складывать цифры, составляющие год рождения или смерти некоторых правителей, то в результате получаются их «порядковые номера». Итак:
Людовик IX родился в 1215 году. Сложите цифры, входящие в эту дату, и получите IX.
Карл VII появился на свет в 1402 году, сумма 1 + 4 + 2 дает VII.
Людовик XII родился в 1461 году, а 1 + 4 + 6 + 1 = = XII.
Генрих IV умер в 1610 году, и 1 + 6 + 1 = дважды IV.
Людовик XIV был коронован в 1643 году, эти четыре цифры при сложении дают XIV. Этот король умер в 1715 году, и сумма этих цифр равна также XIV. Ему было 77 лет, и вновь 7 + 7 = 14.
Людовик XVIII родился в 1755 году, сложите цифры и получите XVIII.
Примечательно, что 18 является удвоенным числом, составляющим «порядковый номер» короля, к которому этот закон был применен впервые, и утроенным числом королей, на которых распространилось действие этой закономерности.
А вот другие любопытные подсчеты.
Падение Робеспьера произошло в 1794 году, Наполеона – в 1815 году, а Карла X в 1830 году.
Поразительный факт, связывающий эти даты, – сумма цифр, которые их составляют, при сложении с числом, выражающим саму дату, дает год падения следующего деятеля. Робеспьер погиб в 1794 году; 1 + 7 + 9 + 4 = 21, 1794 + 21 = 1815, то есть год падения Наполеона. 1 + 8 + + 1 + 5= 15, и 1815 + 15 = 1830, дата отречения Карла X.
Существует странное правило, которое как будто определяло продолжительность жизни папы римского в первой половине XIX века. Сложите его «порядковый номер» с номером его предшественника, прибавьте к полученной сумме десять и в результате получите дату его смерти.
Пий VII стал преемником Пия VI; 6 + 7 = 13; прибавляем 10, сумма равна 23. Пий VII умер в 1823 году.
Лев XII сменил Пия VII; 12 + 7 + 10 = 29. Лев XII скончался в 1829 году.
Пий VIII стал папой после Льва XII; 8 + 12 + 10 = 30. Смерть Пия VIII наступила в 1830 году.
Однако эти расчеты не всегда были правильными. Григорий XVI должен был умереть в 1834 году, но на самом деле освободил папский престол только в 1846 году. Известно, что, согласно древней традиции, любой наместник святого Петра не может править дольше, чем сам Петр, то есть 25 лет.
Вот те папы, что правили дольше других:
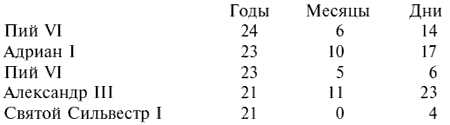
Существует еще одна странность примечательного характера, которой не нужно пренебрегать.
В палате депутатов в том виде, в каком она существовала в 1830 году, было 402 члена, и она разделилась на две части. Первая, в которую входил 221 человек, серьезно заявила о себе во время Июльской революции, другая же партия, в которой состоял 181 депутат, не одобрила изменений. Результатом стало установление конституционной монархии, которая восстановила порядок после трех памятных июльских дней. Партии получили следующие прозвища: более многочисленную стали называть «Хвостом Робеспьера», а другую – «Честными людьми». А теперь, собственно, сам примечательный факт. Соотнесем буквы латинского алфавита, стоящие по порядку, с числами, то есть 1 для A, 2 для B, 3 для C и так далее до Z, которому будет соответствовать число 25. Если мы запишем слева название первой партии с соответствующими числами напротив каждой буквы, а справа таким же образом поступим с прозвищем другой партии[135], то сумма чисел в каждой колонке будет равна количеству членов в каждой из них.

Большинство 221
Меньшинство 181
Всего 402
Некоторые совпадения в датах очень примечательны. 25 августа 1569 года в Беарне и Наварре кальвинисты устроили резню католиков – дворян и священников.
В тот же день и месяц в 1572 году в Париже и других местах убивали кальвинистов.
25 октября 1615 года Людовик XIII женился на испанской инфанте Анне Австрийской, после чего мы можем отметить следующие совпадения.
Имя Луи[136] Бурбона содержит 13 букв, как и имя Анны Австрийской.[137]
Людовику было 13 лет, когда эта женитьба была решена. Анна была в том же возрасте.
Он был тринадцатым французским королем, носившим имя Луи, а она являлась тринадцатой инфантой, которую звали Анной Австрийской.
23 апреля 1616 года умер Шекспир, в тот же день, месяц и год скончался великий испанский писатель Сервантес.
29 мая 1630 года родился король Карл II.
29 мая 1660 года ему вернули престол.
29 мая 1672 года флот был разгромлен голландцами.
29 мая 1679 года было подавлено восстание ковенантеров в Шотландии.
Император Карл V родился 24 февраля 1500 года, в этот же день в 1525 году он выиграл битву при Павии, и в этот же день в 1530 году он был коронован.
29 января 1697 года господин де Брокемар, глава парижского парламента, неожиданно умер в этом городе, а на следующий день его брат-офицер внезапно скончался в Берге, где он был комендантом. В жизни этих братьев присутствовали удивительные совпадения. Однажды офицер, участвуя в битве, был ранен в ногу ударом клинка.
В тот же день в этот самый момент парламентария поразила острая боль, которая неожиданно возникла в той же ноге, что была повреждена у его брата.
Джон Обри упоминает о случае со своим другом, который родился 15 ноября, его старший сын появился на свет 15 ноября, и первенец его второго сына родился в этот же день и месяц.
Во время заутрени 6 апреля 1327 года в церкви Святой Клары в Авиньоне Петрарка впервые увидел свою возлюбленную Лауру. В этом же городе, в том же месяце и в тот же час в 1348 году она умерла.
Делегация, которая должна была предложить греческую корону принцу Оттону, прибыла в Мюнхен 13 октября 1832 года, а 13 октября 1862 года король Оттон покинул Афины, чтобы уже никогда не вернуться.
21 апреля 1770 года Людовик XVI женился в Вене, послав кольцо.
21 июня того же года произошли торжества по поводу его свадьбы.
21 января 1781 года состоялся праздник в честь рождения дофина.
21 июня 1791 года он бежал в Варенн.
21 января 1793 года Людовик XVI умер на эшафоте.
Говорят, что предание, будто число 3 является особым для английской королевской династии, имеет норманнское монашеское происхождение. Оно гласит, что не может быть более трех правителей подряд без переворота.
Вильгельм I, Вильгельм II, Генрих I, затем последовал переворот Стефана.
Генрих II, Ричард I, Иоанн, посягательство Людовика, дофина Франции, который предъявил права на трон.
Генрих III, Эдуард I, Эдуард II, который был низложен и предан смерти.
Эдуард III, Ричард II, который лишился трона.
Генрих IV, Генрих V, Генрих VI; после этого корона перешла к династии Йорков.
Эдуард IV, Эдуард V, Ричард III; корону потребовал и получил Генрих Тюдор.
Генрих VII, Генрих VIII, Эдуард VI; узурпация трона леди Джейн Грей.
Мария I, Елизавета; корона перешла к династии Стюартов.
Яков I, Карл I; революция.
Карл II, Яков II; вторжение Вильгельма Оранского.
Вильгельм Оранский и Мария II, Анна; приход Ганноверской династии.
Георг I, Георг II, Георг III, Георг IV, Вильгельм IV, Виктория. Закономерность «не сработала» в последнем случае, однако в правление Георга IV разразился кризис.
Поскольку я занялся английскими монархами, то добавлю еще одно странное совпадение, хотя оно и не связано с роком чисел.
Суббота была днем дурного предзнаменования для следующих королей.
Вильгельм Оранский умер в субботу 18 марта 1702 года.
Анна скончалась в субботу 1 августа 1704 года.
Георг I почил в субботу 10 июня 1727 года.
Георг II преставился в субботу 25 октября 1760 года.
Георг III умер в субботу 30 января 1820 года.
Смерть Георга IV наступила в субботу 26 июня 1830 года.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Проблема чисел
Проблема чисел Больше всего подобных разногласий мы находим там, где приводятся цифры. Например, в 24-й главе 2-й книги Царств и в 21-й главе 1-й книги Паралипоменон упоминается одна и та же перепись, которую устроил царь Давид. Сравним результаты: «израильтян было восемьсот
Приложение
Приложение Всероссийская научно-практическая конференция «Практика применения законодательства о противодействии экстремистской деятельности и гарантии свободы совести в современной России» Москва, 20 декабря 2011 г.[23] Итоговый документ[24] Мы, участники Всероссийской
Приложение
Приложение Раннехристианские толкования образов запечатанной книги Откр 5: 1 и «книжки» Откр 10 Толкования запечатанной книги Откр 5:
3. Тайны звезд и чисел
3. Тайны звезд и чисел В поисках высшего стандарта, прототипа мирового порядка и гармонии, жрецы устремляли взор к небесам, по которым странствовали недоступные звезды. Тщательные и длительные наблюдения за небесными телами породили учение, которое мы ныне именуем
6. Нет ли здесь природных аномалий или особенностей мира чисел?
6. Нет ли здесь природных аномалий или особенностей мира чисел? Мир полон загадок и сюрпризов. Чтобы убедиться в этом, достаточно заглянуть в последнее издание Книги рекордов Гиннесса или посмотреть телешоу «Невероятная коллекция мистера Рипли», в которых полно странных
Закон больших чисел
Закон больших чисел Предчувствие чьей-то смертиХолт (Holt, 2004) рассчитал вероятность того, что человек может случайно предсказать чью-то смерть. Давайте рассмотрим его логику. Вспомните всех живых людей, которых или о которых вы знаете, о ком вы подумали хотя бы раз (может
Метаанализ и генераторы случайных чисел
Метаанализ и генераторы случайных чисел Самые отдаленные галактики невидимы для невооруженного глаза. Однако их можно обнаружить при помощи согласованных групп мощных телескопов, способных делать тысячи снимков в неделю. Суммирование громадного числа фотографий
ЧИСЕЛ КНИГА
ЧИСЕЛ КНИГА — см. Пятикнижие.
Сравнительная таблица чисел
Сравнительная таблица чисел ЦерковныеАрабскиеРимские единдватричетырепятьшестьседмьосемьдевятьдесятьединнадесятьдванадесятьтринадесятьчетыренадесятьпятьнадесятьшестьнадесятьседмьнадесятьосмьнадесятьдевятьнадесятьдвадесятьдвадесять единдвадесять
Гл. ХХIV. Нелепость доказательств, заимствуемых еретиками из чисел, букв и слов
Гл. ХХIV. Нелепость доказательств, заимствуемых еретиками из чисел, букв и слов 1. Ложность их учения и несостоятельность их вымыслов доказывается еще и тем, что они ищут доказательств то в числах и слогах имен, то в буквах и слогах, а иногда в числах, выражаемых у греков